In his introduction to a book co-authored by the Nobel-Prize winning theoretical physicist, Ilya Prigogine (Prigogine and Stengers, 1984, p. x) Alvin Toffler offers the following commentary on bifurcation:

“In Prigoginian terms, all systems contain subsystems, which are continually “fluctuating.” At times, a single fluctuation or a combination of them may become so powerful, as a result of positive feedback, that it shatters the preexisting organization. At this revolutionary moment—the authors call it a “singular moment” or a “bifurcation point”—it is inherently impossible to determine in advance which direction change will take: whether the system will disintegrate into “chaos” or leap to a new, more differentiated, higher level of “order” or organization, . . . One of the key controversies surrounding this concept has to do with Prigogine’s insistence that order and organization can actually arise “spontaneously” out of disorder and chaos through a process of “self-organization.”

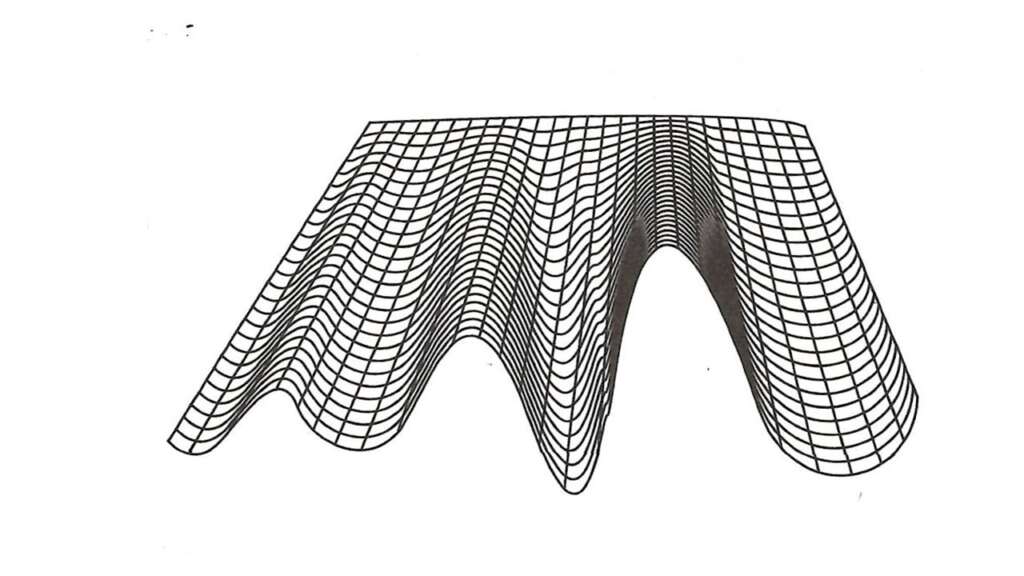
A Warped Plane

The noted biologist, Conrad Waddington (1997) describes this same tendency toward bifurcation in his model of chreods (see Graph One)—warped planes on which objects move in an unpredictable manner. Waddington uses the metaphor of a ball being placed at the top of a slopping plane (thin sheet of metal or plastic). As we bend and warp the plane, ridges and valleys are formed. When the ball is placed on a tilted plane, the inherent dynamics of the plane become evident. The ball will begin to roll straight down the plane until it encounters one of the ridges. At this point a series of oscillations tend to occur. The ball moves back and forth before it eventually begins to roll down one of the valleys and picks up speed again.

Graph One: The Warped Plane